Next: 参考文献 Up: 2 練習課題 Previous: 2.1 非同次境界条件
(1) の代わりに
| (6) |
![]() の場合は、棒をとりまく空気の温度が
の場合は、棒をとりまく空気の温度が ![]() で、
熱的に絶縁がされていなくて、Newtonの冷却の法則に従って、
空気中に熱が逃げる、というように解釈できる。
で、
熱的に絶縁がされていなくて、Newtonの冷却の法則に従って、
空気中に熱が逃げる、というように解釈できる。
![]() の場合は、(やや人工的な想定かもしれないが)
温度に比例した熱が発生する状況と考えられる。
の場合は、(やや人工的な想定かもしれないが)
温度に比例した熱が発生する状況と考えられる。
![]() の場合はリアリスティックであるが、
の場合はリアリスティックであるが、![]() の場合を考えてみよう。
境界条件としては、まずは (5) を考えてみよう。
プログラム作成はかなり簡単な方で、差分方程式を
プリント [1] の (43) から
の場合を考えてみよう。
境界条件としては、まずは (5) を考えてみよう。
プログラム作成はかなり簡単な方で、差分方程式を
プリント [1] の (43) から
| (7) | 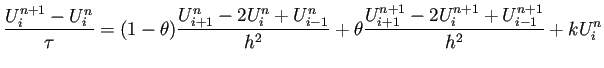 |
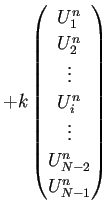
![]() を色々変えて試してみること。実は
を色々変えて試してみること。実は
|
ある
|